-

What is Ultra HDI?
With Ultra HDI, small features come with big decisions. READ MORE...
-

2601shea.jpg
-
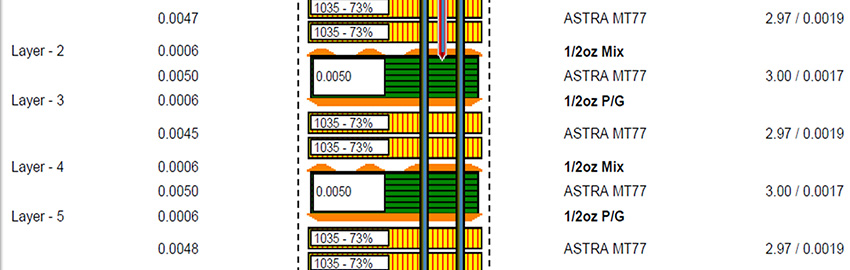
2601roy.jpg
-
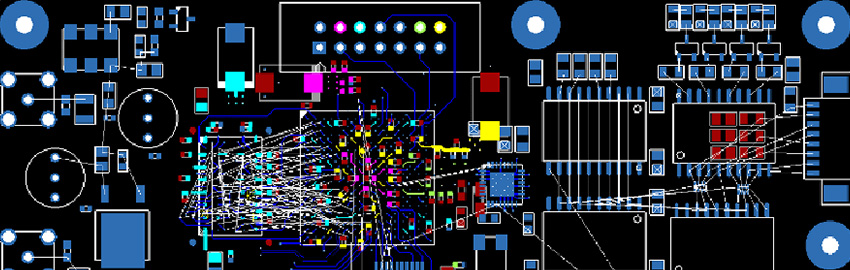
2601designersnb.jpg
-
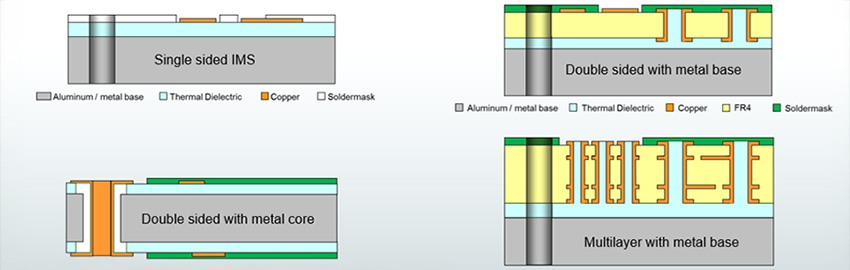
2601boardtalk.jpg
Homepage Slideshow
What is Ultra HDI?
With Ultra HDI, small features come with big decisions.
2601shea.jpg
https://pcdandf.com/pcdesign/images/stories/slideshow/2601shea.jpg
2601roy.jpg
https://pcdandf.com/pcdesign/images/stories/slideshow/2601roy.jpg
2601designersnb.jpg
https://pcdandf.com/pcdesign/images/stories/slideshow/2601designersnb.jpg
2601boardtalk.jpg
https://pcdandf.com/pcdesign/images/stories/slideshow/2601boardtalk.jpg







